This is an extract from the . Previously, (A)lice and (B)obby discussed the importance of creativity in physics.
B: Let’s analyze the creative process with the help of a simplified model:
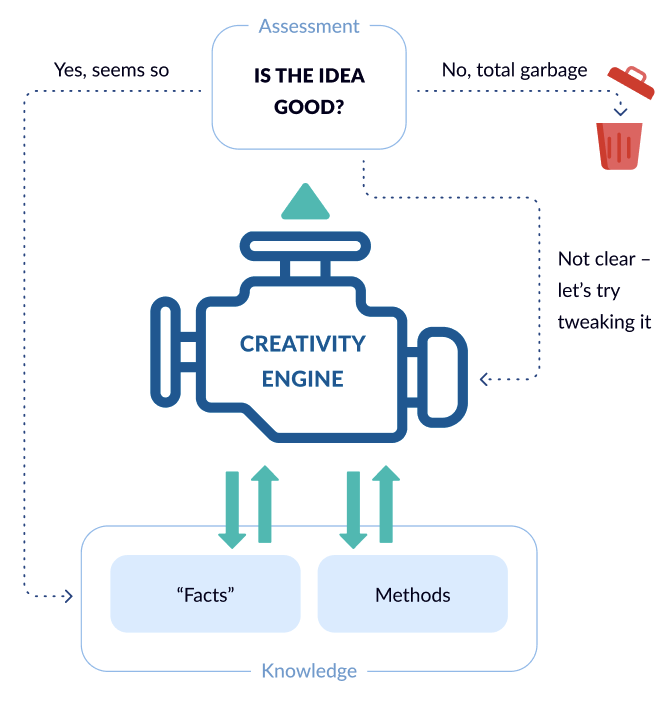
Knowledge is the foundation; it’s the pool of assets we can use for generating ideas. It consists of facts and methods. Facts represent our understanding of the world. They can be wrong, but we need to start somewhere. Facts can be what exists (“there is a table”), what doesn’t exist (“there is no ether”), what may exist (assumptions), and how it all behaves dynamically over time. The facts box also includes the questions to which we need to find answers.
A: Okay, and methods allow us to work with facts?
B: Right, those are all the ways we can combine, re-arrange, discard, connect, disconnect, substitute, adapt, or otherwise manipulate the facts and data. The more of those creativity techniques we have at our disposal, the better.
A: To enrich our arsenal of methods, I guess we should analyze how other physicists did it?
B: Yes, but not only. It’s not limited to the field of physics. Again, it’s all about drawing parallels, and most of them originated in life experiences unrelated to physics. To illustrate this, let’s use the game of chess as an example and discuss its methods, and see how they might apply to physics as well:
- Pattern recognition: As mentioned before, recognizing patterns is crucial in chess. It’s the same in physics. We should find and draw parallels to as many phenomena as we can—no matter in which field of physics—as those may re-appear and become relevant when trying to find solutions in entirely different areas.
- Your gut is your guide: Once you reach a certain level in chess, intuition is key. I remember when I asked a grandmaster why he thought a move I played was bad, he replied with the very insightful “I don’t like it.” Well, I thought, it’s a pity you don’t like it, but how should this be an argument? Chess is a perfectly logical game with clear-cut rules, so shouldn’t there be more transparent reasons why the move was bad? He then went on to deliver those reasons, and it all made perfect sense, but I noticed he was struggling to put it into words. This showed that his correct assessment came from a deep place other than the final explanation he gave. Our understanding is often not words, not even a thought, just a feeling. It’s almost the same in physics. Einstein said, “The intuitive mind is a sacred gift and the rational mind is a faithful servant. We have created a society that honors the servant and has forgotten the gift.” I’ll elaborate on that later.
- Keep thinking a few moves more: Players who find the solution to a chess puzzle sometimes only differ from those who don’t by thinking a bit further. This is related to the already discussed principle of perseverance in physics.
- Questioning rules: Beginners are taught that chess pieces have certain values. For example, a pawn has a value of 1 while a bishop has a value of 3 (and hence, it’s a fair trade if you get three pawns for a bishop). The more advanced the player, the softer those rules: they turn into guidelines instead, first strong, then softer ones. At some point, those are abandoned altogether, and only the specific case matters. Such questioning of ostensible rules is crucial in physics as well. Bohr’s model of the atom, for example, can be a useful introduction to get a first idea of the subject matter. However, after that, if you want to advance on your path of understanding, you will need to let go of the crutches that helped you to make your first steps.
- Switching moves: Sometimes, the moves for a winning combination are known, but they aren’t in the right order. In such cases, switching them is the solution. Being flexible with your candidate moves (approaches) can also be beneficial in many areas of physics. One example is the development of mathematical models in physics, where switching components in equations and trying different mathematical structures can help to find a model that works.
- Just guess: To find candidate moves in chess, it can be effective to simply guess more. That’s because some moves are hard to find, while their evaluation isn’t as difficult. Guessing means “Just assuming I play this move…” which makes the parallel to physics obvious: it’s the postulation of assumptions and seeing what we could derive from that. We should allow such mental freedom and guessing of wild assumptions in physics too, while keeping in mind everything we discussed earlier about assumptions.
- Silent moves: We’re always drawn to the spectacular, and think it’s more likely to be true. Possibly that’s because we can imagine it so vividly, linking it to stronger emotions. That’s why we overestimate the chances of winning the lottery or dying in a plane crash. However, often the “silent moves” in chess are the solutions. Similarly, in physics, the loud and flashy propositions may only be distractions; real progress often comes from subtle insights.
- The solution may lie in the middle: The center of the board has a special significance in chess. Whoever controls it often has the best piece play and good chances of winning the game. Typically, both sides aim to take control of it right from the opening. Also later in the game, if a player is attacked on the flanks, the typical advice is to counterstrike in the center. In physics, the concepts of balance and equilibrium are comparable. You might recall Newton’s principle of “Actio et Reactio” or the concept of energy conservation from your school days.
- Gradual changes can lead to entirely new dynamics: When the allotted time for players to think about their moves is reduced, it’s not that the same principles apply, and that they just occur more quickly. Instead, entirely new aspects emerge. For example, in “bullet chess,” where each player only has 1 minute for all moves, it becomes crucial how quickly the players can move their pieces (the physical execution of it), an aspect that is entirely irrelevant in normal timed chess. A parallel in physics is quantum mechanics, where the “rules” also change entirely at different scales.
- The potential is key: In certain positions, a chess piece has the option to move to two enticing squares, and it’s regrettable that one only has one piece that must decide which square to go to. However, both potential moves are important, as the combined value of having two options can exceed the value of choosing just one of them. In physics, ideas that look like they might be used in various contexts can be valuable even if it’s not clear yet what their final application will be. Their potential is what matters. This concept is reminiscent of situations where a solution exists, but the corresponding problem hasn’t been identified. For instance, when a weak adhesive was discovered, its practical application wasn’t immediately clear. It was only later that its potential for creating removable sticky notes was recognized. More pertaining to physics, the Yang-Mills theory, initially unsuccessful in its goal to explain particle physics, was later repurposed, leading to a beautiful unification of the electromagnetic and weak nuclear forces.
- Admitting mistakes: There are instances where after making a move, you recognize it wasn’t following the right plan. You know that the best action would be to reverse it on the next move. However, psychologically that’s not easy, even grandmasters often struggle with this. Probably that’s because we don’t want to admit a mistake, neither to ourselves nor to our opponents. Yet, sometimes it’s essential to save the game. This is similar to the concept of sunk costs, where you invested resources such as time or money, and this unduly influences future decisions, even though the resources have been spent already, and won’t come back. The most apparent example in physics is to admit that the theory you spent time on doesn’t work, saving you from throwing good time after bad.
- Resisting conventional action: In chess, there are moments when it’s better to not make any committing moves and instead wait. Often the opponent loses patience and makes a mistake. Waiting can be challenging since humans are naturally inclined to act when confronted with problems—the “fight or flight” response kicks in. In physics, a similar principle applies: instead of hastily incorporating new assumptions to validate a theory, it’s often wiser to pause, delve deeper, and address conflicts at their root. In quantum physics, rather than prematurely adapting or altering existing theories, Planck (and later Bohr and Heisenberg) approached the anomalies with patience and detailed investigations, leading to a revolutionary understanding of the microscopic world.
- Learning from the masters: This should be obvious, but often it’s ignored. If you’re in sales, and ask the best salesperson in your organization what makes them so successful, it’s quite likely that they’ll tell you two things. First, they’ll gladly give you some very useful tips. Second, they’ll say something along the lines of “Nobody has ever asked me that.” Isn’t that strange? The best often don’t get asked. You should always think about who the best are in your discipline so that you can learn from them. In chess, it’s the grandmasters. In physics, it’s those who achieved breakthroughs. Listen to them directly, instead of getting it second hand. Don’t worry if it’s an interview from the 50s, 40s, or even older. Physics isn’t like the latest TV serial drama where you need a “previously on…” recap to understand the plot. Not too much has happened since the breakthroughs. Taking it from the horse’s mouth may convey a deeper level of understanding. It may even prevent you from getting caught up in newer thinking frames that haven’t yielded significant progress.
There are several more parallels between chess and the real world[1], but you get the idea.
A: Thank you, I’ll add those to my methods toolbox. However, are you saying that God doesn’t play dice but chess? I think you’re cherry-picking. There are many differences.
B: Yes, physics isn’t chess.[2] My point is that some parallels exist, and being aware of those may help the creative process.
A: Do those methods always help us?
B: No, sometimes they may also lead us astray. Just like with facts, we should regard methods with a good amount of skepticism. That’s also because some methods seem to contradict each other. For example:
- Good moves are sometimes not good enough: It’s tempting to play a good move. However, down the line, it could be decisive that one didn’t play the best move. In the context of physics, before committing oneself to exploring an interesting theory, you may want to check if there are even more promising ones.
- …while decent moves sometimes are (good enough): Spending too much time looking for the perfect move can make you run out of time. In some cases, you have to go for the move that just “does the job.” Such pragmatism is sometimes necessary in physics as well. For example, quantum electrodynamics (QED) was plagued by problems of infinite values in calculations. To overcome those, a process called renormalization was applied, which was a mathematical trick. It looks more like a cover-up than a true solution. It denies perfectionism and isn’t philosophically satisfying in the slightest, but it worked extremely well.
- Keep the goal in mind: In chess, you sometimes have to reach certain strategic objectives, for example getting control of the center, but it’s not clear how. Don’t despair—keep the goal in mind, but be flexible on how to get there. In physics, every attempt to explain a phenomenon by taking an entirely different approach falls into this category.
- …and sometimes forget the goal entirely: I play best when I’m not worried about the outcome and not occupied by whether I’ll win or lose, but get lost in the beauty of playing. At that point, if you ask me “How good is your position?” or “How likely will you win?”, I first have to snap out of my current mindset as it’s an entirely different perspective. This might be a bit surprising, as the goal of the game is to win, right? There seems to be something fundamentally different between “doing it” vs. “talking about it” (describing or assessing it from the outside). Some examples to make clear what I mean:
- How much does a bird know about ornithology (the scientific study of birds)?
- When you do something, get better at it, and then somebody asks you what you’ve learned, often you cannot put it into words, even though you learned a lot. It’s about know-how, not know-what.
- People strive for happiness, but the happiest are often those who are not constantly asking themselves how to become happy. The journey is the destination.
- Jerry Seinfeld (the comedian, not the porn actor[3]) on how to be successful in stand-up comedy: “Boy, if you’re in it for the money, you won’t make it.” You will never have enough stamina if you don’t enjoy the process. We need to do it for the love of it, not for any specific outcome.
That’s why also professional physicists need to stay amateurs in a way: The word “amateur” comes from the Latin word “amator”, meaning “the one who loves”, i.e., who does it for the love of it.
(…)
The book continues to explore creativity in physics. .
—
[1] With the recent advances in medicine, pawns can even become queens. Not sure if this (crude) joke works in English, in German the pawn (“Bauer,” meaning farmer) is male.
[2] While physics (or nature) isn’t chess, it’s intriguing to explore how far the analogy can be taken. One primary distinction is that chess operates on known rules, whereas in physics, we’re in pursuit of discovering the rules. However, even in chess, while the basic rules are clear, the strategies for winning—which can be seen as “rules” in their own right—are still a subject of exploration. Thus, one could argue that despite foundational differences, when examining the emergent properties and higher-level laws, the two realms potentially share significant parallels.
[3] What’s the stronger emotion: the excitement from the thought “OMG, there’s a porn actor called Jerry Seinfeld!?” or the disappointment from learning that actually there isn’t one (I checked)? Maybe it doesn’t matter, because it’s about a different point now: playing, also with the reader’s mind, can be conducive for creativity, as mentioned later in .


