
“The history of physics is one long history of unification.” I never thought I’d quote Michio Kaku, but in this instance, he got it right. Indeed, almost all major breakthroughs in fundamental physics involve some form of unification: the realization that two (or more) phenomena, which appear distinctly different, are in fact manifestations of the same underlying reality.
Our starting position is the opposite: everything seems different. The stone, the tree, and the table, they all appear as distinctly separate things to us.[1] The insight that all objects are composed of the same building blocks (atoms) is a form of unification. The understanding that this doesn’t apply only to inanimate objects, but to living beings as well, is another unification. The same for the characteristics of objects, such as them being hot or cold: it’s just (uncoordinated) movement of atoms that causes this sensation, so yet another unification. And like this it goes on.
The Map of Unifications
(All in one image; move over to zoom, or click to download)
The Map of Unifications
(Less descriptions for easier following of arrows)
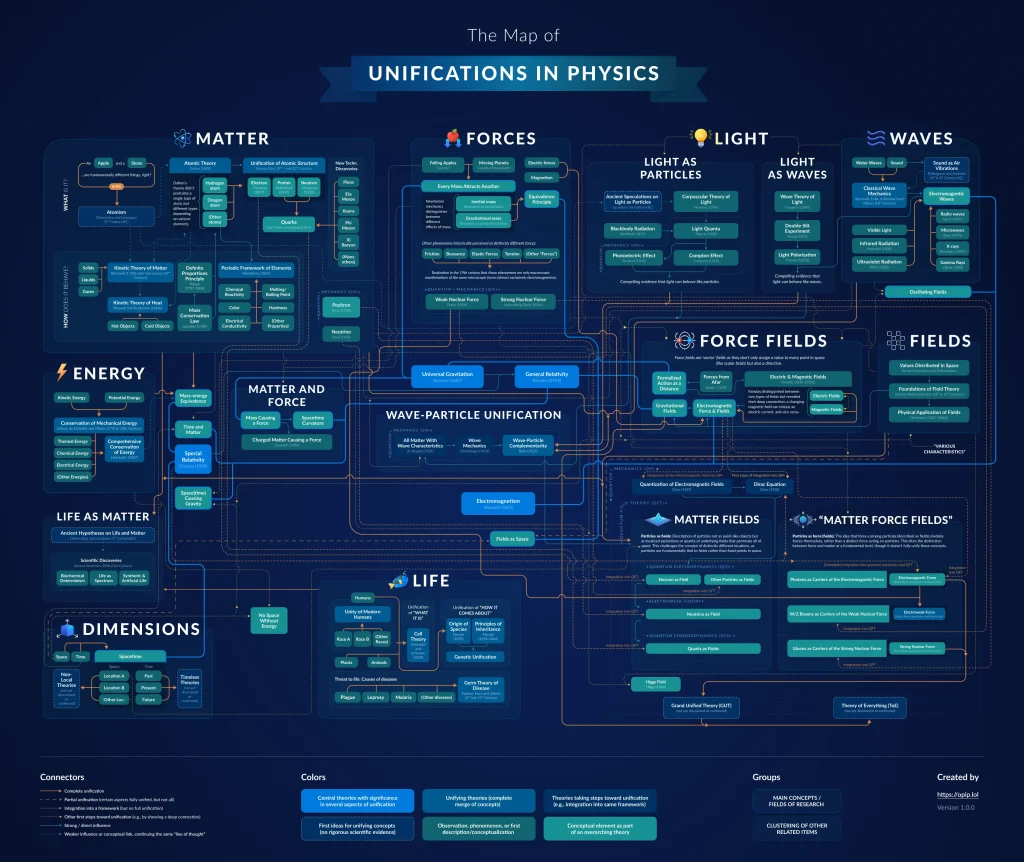
The Map of Unifications
(Spread over several pages; use arrows on desktop, swipe on mobile)











Before delving into the key insights we can draw from the map (which will be referred to as “Unimap” from here on), it’s worth noting that it doesn’t cover all unifications in physics. For instance, one major insight was that the laws of physics are the same in all inertial reference frames. This means that whether we are at rest or moving at a constant velocity, the same physical laws apply, as there is no absolute motion. This principle of relativity, originally formulated by Galileo over 200 years before Einstein, can also be seen as a form of unification, placing these seemingly different scenarios on equal footing. In fact, it represents a higher-level unification, as it applies universally to all physical laws. Depicting this properly this would require the Unimap to be three-dimensional, which is difficult to represent on a two-dimensional surface.
Second, while the Unimap traces some fields back to the first hypotheses in ancient Greece, it could go even further. At some point, both as a species and as individuals, we realized that the waves caused by splashes in a bath are fundamentally the same as the waves in the ocean. As we deepen our understanding of the world, we continuously unify our knowledge—a process that isn’t limited to the field we call physics, as will be explored in more detail later.
Third, there are many other areas in science where unifications have occurred. For example, before the 20th century, geologists believed that continents were fixed in place, and phenomena like earthquakes, mountain formation, and volcanic eruptions were considered separate processes. However, the theory of plate tectonics unified these seemingly distinct phenomena. In mathematics, algebra (which focuses on equations and operations) and geometry (which focuses on shapes, sizes, and space) were treated as separate branches of mathematics until the field of algebraic geometry unified them by showing that algebraic equations can describe geometric shapes, and vice versa. For brevity’s sake, these developments have been left out of the Unimap. (For those who wonder why it’s still titled “Unifications in Physics” despite including examples from chemistry and biology: think unification!)
The Unimap not only falls short of displaying all achieved unifications, but it reflects just a fraction of what still needs to be unified. For example, the Standard Model of particle physics currently considers several particles as fundamental: six types of quarks, each with three “color charges,” resulting in 18 distinct types (along with their corresponding antimatter particles, doubling this to 36). There are also 8 types of gluons, each corresponding to a unique color/anti-color pair, along with other particles like leptons and gauge bosons. In some ways, this is good news for physics, as there is still much to unify. As discussed below, it’s about much more than unifying the four forces.[2]
In other words, the Unimap offers only a glimpse into the history and potential future of unification. Can we still learn something from it?
In the strict sense, unification means merging two separate concepts into one. However, in the context of this article, it is defined more broadly: whenever there are distinct concepts, and we realize the distinctions don’t fundamentally exist, it counts as unification. While combining different entities into a single whole is a frequent way of achieving unification, it isn’t the only one.
An alternative possibility is that two concepts, which initially appear distinct, are on different hierarchical levels, with one being a subset of the other. In other words, if the concepts are regarded as competing, one simply wins. An example of this is classical mechanics and quantum physics. Initially, they seemed like entirely separate and incompatible concepts. However, it became clear that classical mechanics is a special case within the broader framework of quantum mechanics, applicable to larger scales and lower energies where quantum effects are negligible. Similarly, Newton’s laws of motion and gravity are a particular case of Einstein’s theory of relativity, holding at lower velocities and weaker gravitational fields, in which relativistic effects are insignificant.
Another form of unification—in the broader sense of eliminating distinctions—is the following: Let’s imagine we lived in ancient Greece, where people believed in Zeus, the god of the sky, lightning, and thunder, and Poseidon, the god of the sea, earthquakes, and horses. We could formulate the hypothesis that both concepts might, potentially, be called into question. In other words, we can get rid of different concepts by tossing them out the window altogether. A more physics-related example is the ether, once believed to be the medium through which light waves traveled, similar to how sound waves require a medium like air or water. This idea persisted for centuries but was discarded when it was found that light doesn’t need a medium to travel through empty space. In this case, unification occurred by eliminating the ether entirely, simplifying our understanding of light and electromagnetic waves. Similarly, unification often strips away assumptions or models that obscure our understanding of reality.
Strictly speaking, questioning concepts entirely also occurs when two concepts are merged at a higher level.[3] For example, spacetime might initially appear to be a simple merging of space and time—like mixing two types of clay into a single sculpture. However, this analogy falls short in physics. Spacetime is not merely a blend of space and time; rather, it represents a fundamentally new concept. The terms “space” and “time” persist only as historical references, with spacetime operating beyond both. Similarly, wave-particle duality does not imply that light or matter is both a wave and a particle; rather, it indicates that they are neither. We rely on both models to grasp certain aspects, but our familiar ways of thinking cannot capture this new concept. Forgetting this or clinging to outdated expressions can hinder our progress, as further elaborated below.
The Unimap focuses on the outcomes, the results. But how did they occur? First, unifications typically didn’t happen out of the blue. Often it started with the observation that two separate concepts share commonalities or are intertwined in some way. A classic example is Faraday’s discovery that a changing magnetic field can induce an electric current (and vice versa), paving the way of unifying electricity and magnetism by Maxwell. The same happened by de Broglie discovering that matter has both particle and wave characteristics, ultimately leading to their unification. Every time two concepts show a deeper connection, it may be a first clue that there could be potential for unification. Such clues can be very subtle at first and easy to miss. As Isaac Asimov said, “Insight doesn’t come from ‘Eureka,’ but from ‘That’s funny.’”
However, unifications didn’t only result from different concepts facing each other head-on. It also happened quite frequently that the challenge lied somewhere else, and unification was only a means to an end, and perceived—at least at that time—as a side product rather than the core of the matter. For example, Einstein didn’t start out with the objective to unify the concepts of time and space. He was trying to explain why the speed of light remains constant for all observers, regardless of their motion. This led him to re-examine how we think about space and time. Similarly, the unification of all forms of energy under the principle of energy conservation (the first law of thermodynamics) wasn’t the initial goal. Joule and his contemporaries were primarily interested in understanding specific processes, such as the efficiency of engines or heat transfer. There are several other examples where unification wasn’t at the center (at first). However, it could be that consciously moving unification at the core of our efforts may open more direct paths for progress, as will be elaborated below.
If unifications can start as observations of subtle similarities between different concepts, then it implies there is a spectrum of steps toward unification: starting with weak connections that grow stronger until a final unification is reached (though this process is certainly not gradual, but with steps). At the other end of the spectrum—opposite to those first subtle hints—is a reoccurring concept in physics that comes close to unification but stops just short of it: symmetries. Bluntly put, a symmetry means that everything is the same, it’s just flipped, reversed, or positives and negatives are swapped. Examples include matter and antimatter (where charges are reversed but the fundamental structure is the same), spatial reflections (like mirror symmetry, where left becomes right but the laws of physics remain unchanged), or time reversal (where processes play out backward, but the governing rules stay intact). These aren’t full unifications yet, as some differences remain, but they are so close that, when aiming for unification, it makes sense to actively look for these kinds of symmetries.[4]
In terms of how unifications come about, it’s interesting to note that some unifying concepts already existed on paper, without physicists fully realizing their significance. Quarks, for example, were initially introduced as mathematical constructs to explain observed properties in particles, like charge and spin. They weren’t originally thought of as physical entities that could be directly observed. Similarly, when Planck proposed that light might carry energy only in finite amounts, or “quanta,” he saw it as a “mathematical trick” rather than a real feature of nature.
Another noteworthy point about unifications is that achieving them frequently required the development or adoption of entirely new tools or frameworks. Newton could not have formulated his laws of motion and universal gravitation without co-inventing calculus (independently of Leibniz). Maxwell was the first to mathematically formalize the concept of fields in physics, which was essential for developing electromagnetism. Similarly, Einstein applied non-Euclidean geometry to describe the curvature of spacetime caused by mass and energy, marking its first significant application to the physical world. Furthermore, without the application of Hilbert spaces and operator algebra by mathematicians like John von Neumann, quantum mechanics—which paved the way for many unifications—could not have been formulated.
Apart from all those technical aspects of how unifications come about, another factor must not be forgotten: the human element. In the end, it’s always people who are achieving the unifications. Therefore, we need to think about the personal ingredients that make it possible—from physicists’ personal characteristics (especially the willingness to challenge common beliefs and perseverance), the application of creative thinking, the use of intuition, among many other factors. More about those later.
However, one personal aspect should be discussed already now because of its underestimated significance in physics: psychology. Especially, our motivation to look for unifications plays a key role; without motivation to look for unifications, chances for finding them are slim. One example for this can be found in particle physics. In the 1940s, it was already known that the proton and neutron was a core element of the atomic structure (next to the electron). With such few elements, there’s a natural tendency to just accept it as that, thinking this may simply be how nature is. However, when many more particles were found in the 1940s and 50s (different types of mesons and baryons), forming a “particle zoo,” it became much more apparent that it cannot be left like this, increasing the motivation to look for a solution. This was found in form of the quark, which not only unified the newly discovered mesons and baryons, but also the proton and neutron. In this case, the increase in plurality even had a positive long-term effect on unification overall. Without this plurality, we may have just been happy with what we got; but we should never be happy as long as distinctions exist.
The Unimap focuses on unifications, creating the impression that all roads point in one direction: ever more simplicity. At least, it seems to suggest that on a fundamental level. This doesn’t rule out complexity arising from it; simple rules can quickly lead to highly complex outcomes in practice. A classic example is the weather. While the basic interactions between individual atoms may be straightforward, analyzing the overall development of a weather system becomes so complex that even our most powerful computers cannot simulate it. Nevertheless, on a fundamental level, the chart seems to suggest ever more simplicity. Is it true?
One possible objection is that there have been many instances where we ended up with more complexity. For instance, what about Mendeleev’s periodic framework that predicted many new elements, or Maxwell’s electromagnetism predicting several other electromagnetic waves? This isn’t in conflict with the trend toward unification, for two reasons. First, the new elements predicted by these theories are less fundamental than the theories themselves; they are merely a result of them, as illustrated by the example of the weather (also as discussed below in the principle of emergence). Second, those phenomena were already unified at the time the theory was developed. Maybe it could be called an ex-ante unification or pre-empirical unification. In any case, no complexity was added on a fundamental level.
However, what about the discovery of new elements we still consider fundamental today? As mentioned above, the Standard Model of physics comprises quite a few of them. The key question is whether these elements are the final say on the matter, or just a temporary concept until a better theory is found. If history is any guide, it’s the latter. It’s important to remember that almost every concept was considered fundamental until unification was achieved. It’s natural to perceive our current moment as the pinnacle of what can be known, but we must always remember a central ingredient for progress in science, which goes by the name of humility.
Another way to think about the apparent increase in complexity at a fundamental level is that this could simply be a consequence of more advanced technical equipment, enabling us to identify these elements for the first time. Imagine if you had unified electricity with magnetism in the 19th century and traveled to a remote village to announce your discovery, only to be met with the response that you have, in fact, increased complexity, as they had never experienced electricity or magnetism in the first place. In other words, plurality can arise because we’re looking more closely for the first time.
The conclusion appears to be that complexity on a fundamental level arises only in two scenarios: when we discover new elements due to advancements in technology, or as temporary concepts that have almost always been unified eventually. In other words, the arrow of unification indeed seems to point in only one direction. And now that we’ve discussed the what, who, and when of unifications (Unimap), as well as the how (ways of unification), it’s time to ask the mother of all questions…
Why doesn’t nature make a fundamental distinction between separate elements, and that’s it? Before discussing potential answers, it’s worthwhile to reflect on the question itself. Despite unification being a major force for progress in physics, this question hardly ever gets asked. Googling for “Why is there unification in physics?” returns almost no results. It seems to be a complete blind spot not only of our understanding, but also in our motivation to understand. We’re not interested in it at all, our focus lies elsewhere. For comparison, the question “How old is Taylor Swift?”[5] generates hundreds of results (answer: 34, as of September 18, 2024). Why don’t we care about why unifications in physics are possible?
One reason could be that the question of why sounds suspiciously philosophical to many physicists. The “shut up and calculate”-attitude—coined by N. David Mermin and often associated with Richard Feynman—is widespread in the physics community. This is lamentable, as the question of why is inevitable if we aim to get to the bottom of things. There’s a good reason why many of the most eminent physicists had a very keen interest in philosophy. Separating the world into questions of physics and philosophy (which, by the way, also goes against the idea of unification) and dismissing the latter as irrelevant, is dangerous and has been shown to be incorrect, as exemplified by Bell’s Theorem. This will be further explored in a future post. For now, let’s return to the main thread.
To understand why unification occurs in physics, it’s useful to explore in greater depth what exactly happens when we unify. As mentioned before, the analogy of merging two types of clay into a single sculpture doesn’t apply. It also falls short for a reason other than the one previously stated. The artist who takes the clay is changing it actively into something new. However, when Einstein unified space and time, those elements remained unchanged. Nature stayed untouched and continued as it has always been. What happened was that we corrected a flaw in our understanding. Previously, we made a distinction where fundamentally, there was none. Or, in other words, we corrected our model of the world.
Viewed from this perspective, the long history of unifications can be seen as the confirmation and re-confirmation that the distinctions we make are fundamentally flawed. Will we ever reach a point where we can say, “Now this distinction, we can be sure it’s fundamentally correct”? It hasn’t happened yet, and in the following chapters it will be argued that it never will. And that therefore, unifications must continue to be possible as they are just the reversal of the flawed distinctions we have created.
To understand something deeply, we need to know how it came about. How did our models of the world evolve? First, organisms developed methods to enhance their chances for survival and reproduction by using external signals to adjust internal behavior, both to use it to their advantage (e.g., finding food) and to prevent threats (e.g., becoming food). Those methods started as very simple and immediate, reflex-type reactions to environmental stimuli. As time passed, they became more sophisticated and complex, eventually leading to a process known as “thinking.” This involves creating an internal model of the world to simulate reactions to external stimuli—essentially doing dry runs—before selecting the option assessed as most beneficial. (And along with it, an incentive system of pleasure and pain evolved to guide organisms in making such choices—which gives us all the headaches we now have. See The History, Present and Future of Happiness).
How good is this model? Naturally, the answer heavily depends on which type of organism we’re talking about, as the models vary significantly. To begin, let’s consider a living being that is more than a simple cell yet remains relatively simple from a human perspective: an insect. We don’t know exactly how an insect perceives the world, but at least in some respects, we can be sure that it has a much more basic level of understanding than we do. For instance, an insect may sense a beam of light and adjust its behavior accordingly. However, it doesn’t understand what’s going on, at least not to the extent that we do (e.g., how light spreads, its speed, etc.). Moreover, it’s not that the insect doesn’t know this because nobody has told it yet; we could be the best explainers in the world, but the insect would just stare at us with big eyes and not understand. Its brain is not designed for this level of sophisticated comprehension; it’s simply beyond its capability. This applies to many insights that appear straightforward to us. On an IQ test, an insect would score a dead flat zero.[6]
However, before mocking the insect’s limited grasp of the world too much, we should be a little careful. As it so happens, we share up to 60% of the insect’s genes.[7] It’s plausible to argue that the 40% difference allows us to have a much more comprehensive and deeper understanding of the world. However, it must still be in the same range, category, and dimension as that of the insect, which gives us a first hint of how limited our understanding must be.
A key reason why we believe our models are fundamentally correct is that they seem to work very well. However, is that really the case? Several objections could be raised, which will now be addressed in turn.
First, it’s important to note that the statement “but they work so well” could have been made at any point in history, regardless of how primitive the models may seem from today’s perspective. The models we’re applying now always appear to work very well, as we’re comparing them to our previous ones. We can only look into the past, never the future, which carries the risk that we think our models are the best they can be. As noted earlier, the present moment always feels—and has always felt—like the most enlightened possible. But history has repeatedly shown us that this belief isn’t accurate.
Second, when we conclude that our models work well, we base it on what we can observe and measure. That may be only a small fraction of “reality.” It would be more accurate to say that they work well within the realm of what is accessible to us, which underscores their limitations and distances them from an objective truth.
Third, what’s the alternative? It would be that our models didn’t seem to work well, which wouldn’t make any sense. They evolved over millions of years, getting better and better to help us navigate the word. Naturally, they give us the impression that they’re fantastic—they’d be lousy if they didn’t.
Fourth, science has advanced enough to know that when we look beyond the everyday world we live in—for example, by leaving our “medium-sized” world and diving into the worlds of the very large or very small—our models break down. This becomes evident when we observe phenomena in the macro world that don’t correspond to our everyday experience (such as light bending around large objects). It becomes even clearer in the micro world where fundamental concepts like time and space cease to make sense at some point (at the Planck Time of 5.391 × 10−44 seconds and the Planck Length of 1.616255 × 10−35 meters).
It might be objected that while this is true, it takes us a long way, and only stops working at incredibly small scales. However, this is a matter of perspective. How small is the Planck Length really? It’s certainly small compared to the everyday dimensions we’re used to. But it’s 10 to the power of 35. Thirty-five. If we count it in millimeters instead of meters, it’s already down to the power of 32. It wouldn’t be difficult to come up with numbers larger (or smaller) than that. It’s reminiscent of Ephraim Kishon’s humorous story “Jewish Poker,” where the goal of the game is to think of a number higher than the opponent. It wouldn’t be difficult to do a better job than 35. From that angle, our models look rather shallow.
The superficial nature of our models also becomes clear when drawing the Unimap. At first, expressions like matter, forces, and light appear quite solid (literally so in the case of matter). However, the more one dives into it, the more vague the expressions become. It slowly becomes clear that the accurate way to phrase it would be “what we call matter,” “what we call forces,” and so on, which isn’t feasible to write on the Unimap. Consequently, the idea arose to place the expressions in quotation marks. However, almost all expressions on the Unimap then had quotes, which looked ridiculous. As a result, they were omitted, but it’s important to remember that these terms are merely vague and fundamentally flawed attempts to describe nature.
Another reason why we believe that our models are working so well is that they are making correct predictions. That is, after all, the way we assess the quality of a model. If the predictions are right, it’s a good model (which inevitably has the ring of “true” in it); and if it doesn’t make good predictions, it’s bad. However, we must not forget that the tool we use to assess whether the predictions are right is often the exact same tool we used to make predictions in the first place. For example, we see that the grass is green many times, so our model predicts that the next time we look at the grass, it will also be green. And lo and behold, this turns out to be correct. However, our brains make up the perception of green, which was true both when the prediction was made and when we verified the outcome. In that sense, it’s a bit like a self-fulfilling prophecy.
In general, confusing a model that makes correct predictions with fundamental truth is a common thinking mistake. For example, Newton’s laws of motion work extremely well and are sufficient to send a man to the moon.[8] At the time of Newton, there were only a few phenomena they couldn’t explain. We had to look as far as the precession of Mercury’s orbit or the bending of light around massive objects like stars to find such cases. In terms of explaining our observations, Newton’s model could probably be described as 99.99% accurate. However, this shouldn’t be mistaken for being fundamentally correct. As it turned out, Newton’s model wasn’t 99.99% correct, nor 50%, nor 1%. It was entirely wrong in how it fundamentally understood gravity. Einstein had to come up with an entirely new understanding to account for those “corner cases,” reflecting a complete paradigm shift.[9]
Another misconception is that models providing value are also the ones that are closer to the truth. Sometimes there is a correlation between the two, but often there’s not. If we had to choose between a model that is closer to the truth and one that adds value, we almost always opt for the latter. A good example is the belief in a higher power without evidence. Its utility can be manifold: as an endless source of hope, transforming the fear of dying into looking forward to eternal bliss, and being aligned with friends and family, among other benefits. How much value we get from such a model varies from person to person, depending on one’s genes, upbringing, personal experiences, social circle, and other factors. However, if circumstances allow us to gain significant value from the model, it’s hard to imagine anyone not taking advantage of it. Sometimes, abandoning logic can be the most logical thing to do.
The idea that “truth” or even “closer to truth” doesn’t matter much—or may even be harmful—also becomes clearer when we consider the example of the insect again. As mentioned before, at least in certain respects, insects know much less about the world than we do. However, their model is extremely successful—arguably much more than our own.[10] Let’s imagine we were the insect, relying on our “superior” model. We’d probably not even last a day. If insects could talk, they’d probably say, “Leave me alone with your ‘better’ (worse) model.” A model can never be objectively good or bad, the assessment must always be made in the specific context. That further emphasizes the distinction from an absolute truth.
The idea that a true reflection of the world could hurt us—and that our models might develop to hide this truth—also becomes clear when we consider the purpose of our subconscious mind. One of its core aims is to filter out the information our conscious mind doesn’t need, so that we’re left with only the key bits of information required for making conscious decisions. For example, light reflected from an apple can contain important information about whether the apple is edible. However, if our conscious mind were flooded with millions or trillions of light waves, it would lead to information overload, making decisions impossible. Therefore, our subconscious mind created a heavily simplified model, inventing an effective method of distinction that we call color, greatly facilitating our decision-making (eat the green apple, leave the brown apple).
Perhaps that’s the reason why distinctions are at the core of our models; they enable us to make another important distinction: selecting the most beneficial actions. Even if not true on a fundamental level, in the everyday world, we’re well advised to keep separating an apple from a stone, so that we don’t bite into the stone, and between a teddy bear and a lion to ensure we don’t run away from the former and hug the latter (although sometimes, that works out fine). That these distinctions aren’t fundamentally true is irrelevant.
In this context, the principle of emergence is crucial. A classic example is buoyancy: a ship is floating on water and doesn’t sink. If we go down to the level of single atoms to explain it, we may report back, “I don’t see any floating ships here.” Of course we don’t. The atoms collectively cause the phenomenon in its entirety, but we still cannot explain it on that level. It only manifests, and “exists,” in our larger, everyday world, which is the relevant one for us. Put another way, we have to deal with emergent phenomena because we’re one ourselves. So far, almost all phenomena can be considered emergent, and not really existing on a fundamental level.
Incidentally, arguing how flawed the human model is isn’t even necessary to make the point. It’s already sufficient to acknowledge that it’s a model. Any model is always created and constructed. And no matter how good it is at modelling something, it is never that something itself. Both Alfred Korzybski’s “The map is not the territory” and George Box’s “All models are wrong, but some are useful” reflect this well. The conclusion from this is that we will never get to know the truth; the best we can ever strive for is to be less wrong.
The previous chapter contains an assumption that it itself refutes. It argues rationally for the shortcomings of our models, implicitly assuming that good arguments are sufficient to convince. However, as hinted, logic is just a tool that—like any other tool—we use when it suits us, and not if it doesn’t. If what is said goes against our current models, thereby threatening the value they provide, we quickly dismiss the arguments, regardless of their quality. We may still come up with ostensible counterarguments to maintain the impression of having reached a rational conclusion, but the decision has already been made. In other words, psychology plays a key role once again.
There are also mechanisms at play that seem positive at first but, in fact, make it more difficult to question our models. For example, improving our understanding and finding solutions helps us navigate the world better, which is why nature rewards us. We feel good when we gain insight, even before we use it. For instance, Einstein reportedly described his discovery of the equivalence principle as the happiest thought in his life. However, there’s a drawback to it too: if understanding is rewarding, then questioning our existing beliefs can be painful because it jeopardizes our previous gains.
We also cling to our models as the ultimate, objective truth because we tie our sense of self-worth to them. If the insect’s model of reality isn’t inherently worse than ours, does that mean we’re diminishing ourselves to their level? Admitting that we’re not at the center of the universe or not a divine creation (conveniently placing humans at the highest position, giving ourselves permission to reign over all others) can be uncomfortable. The Enlightenment began over 300 years ago, yet it looks like it will still take some time to fully sink in.
Related to this, there’s the ego. We just hate getting proven wrong. This is especially true because it feels like a threat to our social status. Evolutionarily, this makes sense: higher social standing used to correlate with better chances for reproduction (and still does—“Get laid like a rockstar”). This dynamic is particularly pronounced in men, which may explain why they tend to have stronger egos and greater difficulty challenging their views.[11] The social factor is even clearer when we consider that we’re much more willing to change our views when alone, rather than in a group. Admitting we’re wrong in front of others can feel like a loss of status, especially in competitive environments where hierarchy and reputation are key to personal success.
Another challenge lies in the fact that being wrong implies—at least in our perception—that many of our previous decisions were incorrect, as those were based on the old model. On a rational level, we may even fully understand the concept of sunk costs and that they shouldn’t impact our future decision-making. However, emotionally this is difficult to accept, causing us to instinctively reject any new insight that questions the many decisions we’ve made so far. This becomes more challenging with age, as we’ve made more decisions based on our old models.
In summary, being an elderly male in an exclusive group of friends looking back at their life’s achievements doesn’t seem like the winning combination when it comes to questioning current thinking frames. However, to be fair, it’s difficult for anyone accustomed to the current models. Perhaps generational change is needed to overcome these challenges, as Max Planck hinted when he expressed the idea that “science advances one funeral at a time.”[12]
The essence from the above is that while it is hard to accept, our models are fundamentally flawed. And with them being flawed, the distinctions they make are flawed as well, allowing to conclude that continued unifications are an almost certain possibility.
Most scientists probably agree that unification plays an important role in the progress of fundamental physics. However, it’s crucial to understand just how significant it really is. The following thought may give a first glimpse of it: let’s say we removed the title of the Unimap, made the unification arrows a bit thinner for less emphasis, and then showed it to someone and asked them what it depicts. It’s not unlikely that they’ll say it reflects progress in physics overall. That’s probably because it contains all the key milestones such as Newton’s laws, Maxwell’s electromagnetism, both of Einstein’s theories of relativity (collectively referred to as the “Big Four” going forward), the key aspects of quantum mechanics, and much more. This is surprising, considering that this wasn’t the purpose of the map at all—it was solely about unification. If those two are so aligned, it must be telling us a deeper story.
This is further supported by the observation that the Big Four theories didn’t just influence one aspect of unification but several. Initially, when the Unimap was first drafted, these theories were placed within one of the main areas—matter, forces, and so on. However, as their wider influence became more evident, it was necessary to remove them from any single area. Instead, specific aspects of each theory were highlighted, with lines connecting them to the main theory, as shown in the current Unimap. From this, a hypothesis can be formed: the more aspects a theory unifies, the greater its significance and impact—an insight that may be crucial for identifying new key theories.
It’s worth noting that unifying theories don’t just unify; they also build on prior theories that unified other elements, thereby reinforcing the significance of the previous unifications. For example, special relativity’s unification of space and time would have been unthinkable without the prior unification achieved by Maxwell’s electromagnetism. Thus, the latest theories represent the pinnacles of a mountain of previous unifications. From this perspective, the saying “on the shoulders of giants” might be more aptly rephrased as “on the shoulders of past unifications.”
The significance of unifications is also highlighted when we recognize that they not only deepen our understanding of unified phenomena but also reveal new ones that emerge from the post-unification framework. These are the ex-ante unifications mentioned earlier, such as how Maxwell’s electromagnetism predicted additional electromagnetic waves, or how Einstein’s general relativity predicted gravitational waves. What may initially appear to be a deeper understanding of two phenomena ultimately leads to a more comprehensive map of reality, extending far beyond the original concepts.
But now, we must ask why unifications play such a crucial role. For that, we should first seek to understand understanding itself. What does it mean to “understand”? At its core, understanding means knowing how something came about, enabling us to extrapolate that knowledge to make future predictions. And how something came about is often the result of entirely different dynamics than what emerges on the surface. We need to get to the bottom of things, which the term fundamental physics expresses.
So how do we get to the bottom? Here again, the why question is crucial. Children ask a series of why questions which is how they learn. For example, a child may know the phenomenon of rain, but may hear a sound that they don’t associate yet with rain. When the child understands why there is the sound, it links together the two separate phenomena of rain and the sound. This allows the child to make predictions and act accordingly (“When I hear that sound I won’t go out; I’d get wet”). The child unified the previously separate phenomena of rain and the sound it creates. This demonstrates that the why question, which is essential if we want to learn, is inextricably linked with unification (and vice versa). From this angle, it’s a bit of a contradiction if physicists work on fundamental physics but have a hostile stance toward the why question.
Also in this example of the child, the unification can be seen as correcting the misconception that two phenomena are entirely separate and unrelated. This illustrates the value of unifications: they eliminate bugs in our models, and models with fewer bugs tend to work better. The question is: how does unification compare with other methods to improve our models? Or, phrasing it more directly: is there even any other method?
Did all major enhancements of our models in fundamental physics involve unifications? To explore this question, we can take a few examples where unification doesn’t look like it played a key role and analyze if maybe there was still unification on some level.
For example, what about the insight that Earth moves around the Sun and not the other way around—where’s the unification there? Here, we need to look at the broader picture. The underlying theory (which explains it well—we don’t have to look at early philosophical thoughts in that direction) isn’t just about Earth and the Sun. The heliocentric model unified planetary motions by showing that all planets follow similar paths around the Sun. It replaced the more complicated geocentric model, where different rules applied to different celestial bodies. It’s natural that we zoom into the conclusion that affects us and our worldview (“What? We’re not at the center of the universe?”), but by doing this, we’re running the risk of overlooking that this revelation is only a part of an overarching, unifying theory.
What about Max Planck’s postulation that light may only carry energy in discrete amounts, or “quanta”? Even though it led to quantum physics, which sparked a unification spree, this insight wasn’t a unification itself—or was it? In fact, it might be regarded as one of the biggest steps toward unification possible. Unification means moving toward simplicity, reducing the many to the few (or even “one”). Looked at from this angle, unification has an opposite, an antagonist so to speak, which is infinity. Quantization is nothing other than dissolving the idea of the continuous—be it in space, time, or whatever—which implies infinity, as it can be chopped up into ever-smaller chunks, endlessly. The relationship between unification and infinity will be explored in more detail below.
One more example: what about Schrödinger’s breakthrough with his wave equation—is there even a smell of unification? No, there is no smell; it reeks of unification, as it unified the concept of matter with the concept of waves. Before this, matter and waves were treated as fundamentally different. Particles were seen as localized objects with definite properties, while waves were considered extended phenomena like light waves. Schrödinger’s wave equation merged these concepts by showing that particles, like electrons, could also behave as waves, introducing the notion of wave-particle duality (which was later truly unified by Bohr’s insight that it isn’t a duality at all but something uniform, as mentioned above).
This shows that unification almost always seems to have its fingers in play, even though it may not be in focus, perceived as only secondary, or be so unnoticeable that even the creators of the theories may not have recognized its role at all. Did Planck think in the slightest about unification when he introduced the idea of quanta, or Schrödinger when he formulated the wave equation? Chances are they didn’t—and thus were unaware of the true driver of progress.
With this thought, this article goes beyond the description or explanation of unifications by proposing another unification: a unification of methods, positing that various methods of progress in fundamental physics share unification as a common denominator. This means that not only is unification understanding, but understanding is also unification. Or, in other words, the unifying element that unifies all methods of progress is unification. The utility of this is that it places unification at the forefront of our attention, potentially paving the way for more direct ways for progress, as argued further below.
Given the above reasoning, most people likely agree that unifications must continue to be possible. But is there a limit? There’s one type of unification that may be considered the ultimate unification, which even the strongest unification enthusiast finds hard to wrap their head around. It’s questioning the distinction between existence and non-existence, 0 and 1, to be or not to be. Even if our perceptions trick us and we’re creating distinctions in our minds, they must come from something that “is” rather than “is not,” or not?
The reason we have difficulties questioning the existence/non-existence dichotomy is because it’s so inextricably linked to our understanding of reality. For example, let’s say we’re thinking about an apple on a table. Then we look at the table and see there isn’t any apple. The apple doesn’t exist and is not real. If we question a basic logic like this, it feels as if the ground under our feet is pulled away, leaving us nothing to stand on or hold on to. Even our declared goal in physics to “get to the bottom of reality” stops making sense because the term reality itself gets questioned. This is very hard to process psychologically—not only because we’d have to give up beliefs we hold dearly, but because it instantly raises the question how we could describe the world if even that basic assumption is wrong.
However, we should remind ourselves that the big breakthroughs in science were always incredibly hard to accept at first. Is questioning the 0/1 paradigm really that much harder to digest than that the Earth is round, floating around in space, and not at the center of the universe? What about time and space not being absolute? Also, the proposition that we share the same ancestor as the blobfish (take a look in the mirror here) wasn’t easy to swallow, to say the least. Of course, this refers to how hard it was to accept these ideas at the time, before they became common knowledge. Most insights look obvious in hindsight. That they were surprising at first isn’t surprising at all; new discoveries must be very surprising, as otherwise we would have already found them.[13]
But still… existence and reality not existing, really? Why do we have those notions at all, then? The answer might be the usual: they could be emergent phenomena. It’s difficult to understand, but we should remember that this just means it’s hard to grasp with a brain that wasn’t designed to understand such things. Our brains have developed to deal with emergent phenomena, as that’s what’s relevant for our reproduction. This might be easier to accept if we remind ourselves that we’re only discussing the distinction between existence and non-existence not existing on a fundamental level. In our everyday world, we can still treat it as real. It’s similar to the example of buoyancy: on a fundamental level, it doesn’t exist. But that doesn’t mean it doesn’t exist in our reality—floating ships are very real in our world. In other words, “reality” is still valid, it just applies to a certain range. For the world we live in, reality is still “real,” as paradoxical (or tautological, paradoxically) as that may sound.
These thoughts could easily be dismissed as drifting into pure philosophy, if not for the fact that current physics already says it. In quantum mechanics, particles can exist in “superpositions,” meaning they don’t have a definite state of being until observed. Moreover, quantum mechanics hammered our familiar, much-cherished concept of particles as hard, pinpoint elements into complete mush. When particles were discovered to behave like waves, the idea of particles being fixed at definite coordinates began to dissolve. And with the view of particles as fields, the indeterminacy was complete—now they can be seen as both everywhere and nowhere.
To reduce the risk of our heads imploding when thinking about those concepts, there are a few things to keep in mind. The first is that it’s not necessary to intuitively understand it to work with it. We can just postulate it, and see where it takes us, similar to how quantum physics has done this quite successfully for over a hundred years. Second, we’re not forced to resolve this ultimate distinction immediately. We have enough fodder in physics to resolve all the other distinctions we’ve made. The question is: how can we achieve it?
To succeed at unification, it’s helpful to know what needs to be unified. The Unimap is a first attempt to provide an overview by not only giving a historical account of successful unifications, but also by displaying outstanding potential unifications. Any concepts that are still considered distinctly different are candidates for unification. Moreover, the map may provide hints for prioritization: elements that already show a deep connection (dotted lines) could be primary candidates for unification, as first steps have already been made.
The Unimap demonstrates the value of the big picture in another way too: it immediately makes clear that we cannot be at the end of the road when it comes to unification. No expertise in physics is required to come to that conclusion, and no detailed explanation why this must be so (as provided above); common sense is sufficient. The fact that eminent physicists expressed doubts with regards to the possibility of future unifications (Hawking, Dyson and others[14]) shows that the layman with the big picture can have an edge over the expert without it.[15]
Another thought that underscores the importance of the big picture view is this: as mentioned earlier, the Big Four theories couldn’t be confined to any single domain because they impact multiple areas. This means their scope is inherently broad. Crucially, these theories didn’t just unify elements within individual areas independently; they had to unify elements from multiple areas at the same time, as they wouldn’t work otherwise. This may also explain the true challenge: unifying elements within a single domain is difficult but achievable, whereas unifying elements across different domains is a far greater task, requiring a “think big” mindset.
The Unimap may also help to assess today’s unification efforts, which currently focus almost exclusively on merging the known forces. The “Grand Unified Theory” aims to unify the electromagnetic force with the weak and strong nuclear forces, while a “Theory of Everything” takes this a step further by including gravity. From a unification standpoint, those efforts should be applauded. However, they overlook many other areas of potential unification. So, why is it called a “Theory of Everything”? It’s reminiscent of the baseball championship between teams from the USA and Canada which they humbly call the “World Series.”[16]
The risk of this narrow focus is not only that we may overlook other potential unifications, but it goes deeper. If we make it look like there are only a few loose ends to tie up, our approach is different. In such a mindset, we’re much less likely to fundamentally question our existing models and methods. Instead, we build on them and try to find solutions by tweaking them a little here and there—which hardly ever worked in physics when big unifications were called for.
In the same spirit, we should also assess previous unifications holistically. Maxwell’s electromagnetism is commonly seen as a unification of forces, but it could just as well be viewed as a unification of the concepts of electric and magnetic fields. This was a major discovery, as it revealed that oscillating electric and magnetic fields could propagate through space as electromagnetic waves, linking light and electromagnetism. This conceptual leap laid the groundwork for modern field theory, which has since become the dominant framework for describing physical phenomena in areas such as quantum field theory and general relativity.
Incidentally, a pure focus on forces should also be regarded skeptically because the concept of force still implies a dichotomy: the force itself and something it acts on—such as matter. This does not mean that attempts to unify the forces are futile; they could indeed bring us a step closer to the truth. However, even if they succeed, they will not mark the end of the story and thus not constitute a “final theory,” as sometimes suggested.[17] This is yet another consideration we should keep in mind before declaring the so-called “Theory of Everything” the holy grail of physics.
Another risk that emerges with a narrow focus on the unification of forces is that new theories may create as many loose ends as they resolve—or even more. For example, even if string theory succeeds in unifying the four forces (and that’s a big IF), but it needs to introduce seven more dimensions to achieve it, then from a unification perspective, the outcome could be seen as a net loss.[18]
[For the record, this critique of string theory shouldn’t be mistaken for taking aim at a theory that hasn’t delivered in a long time. It’s always easy—and often a sign of weak character—to mock something or someone currently struggling. The issue here isn’t string theory’s lack of progress, but rather the approach it takes. To support this point, an approach should be lauded that also hasn’t produced results yet, despite many years of effort: in the last 30 years of his life, Einstein pursued a unified theory that postulated matter is made of spacetime. This direction is much more in the spirit of unification and likely deserves further development. Maybe Einstein’s shadow will stretch further than we realize today.]
To cheer up string theorists again, it’s worth noting that alternative approaches sometimes fare even worse when it comes to unification. Loop quantum gravity, often considered string theory’s main competitor, moves backward by proposing that space and time are fundamentally different entities. Although this theory was developed long after Einstein’s death, there’s little reason to speculate on what he might have thought of it. In any case, many theories aiming to unify the four forces lack the broader perspective, diverging from the ultimate goal: an overall more unified understanding of the world.
Keeping the big picture in mind is valuable also because diving into the details rests on the assumption that the higher-level concepts we’re diving into are correct. However, there is no guarantee they are, and probably they’re often not, no matter how obvious they may seem. It’s like taking a wrong turn and going down a long road without realizing it’s a dead end. In such cases, no matter how intellectually brilliant we are with the details, it will be all in vain. Therefore, we must always be aware of our assumptions and minimize them as much as possible. This is the true value of Occam’s Razor, the principle that advocates for simplicity by striving to take the path with the fewest assumptions.
Another assumption that may slip in unnoticed is that we’re working on the right problem. Often in physics, progress came from finding solutions to problems that many didn’t even realize existed. This is discussed in the post “What’s the Problem?” and doesn’t need to be repeated here. The key takeaways are that long periods without finding a solution may point to the problem definition being wrong, and that finding the challenge is the challenge. Also, what makes this issue especially devious is that it can feel good to find solutions, even if they’re for the wrong problems. This further emphasizes the importance of the big picture, as it improves our chances of working on the right problems.
Additionally, the importance of the big picture stems from the fact that, paradoxically, solving problems often requires a certain distance from them. It’s natural to move toward a problem to fix it, but it’s often not the right path. For example, when we’ve written a first draft of an essay, we could look at every word individually and consider how to optimize each one, but that will miss most of the crucial elements (overall structure, clarity, flow, etc.). While the essay is made up of words alone, we still won’t find the solutions at their level. It’s not only the problems that are emergent, but the solutions need to be as well—and for this, the big picture is crucial.
To avoid any confusion, focusing on the big picture doesn’t mean being superficial. There’s a lot of depth to be explored at that level, without needing to zoom in on individual elements. It’s still detailed, but a different kind of detail. In his famous 1959 talk, “There’s Plenty of Room at the Bottom,” Richard Feynman pointed out that there’s a lot of space at atomic and nuclear scales (since even solid objects are mostly empty space), enabling what would later become known as nanotechnology. Mirroring that, it could be said that there’s not only plenty of room for exploration down there, but plenty of room for exploration up there. In a way, we need to specialize on the unspecific.
So far, the big picture has received a lot of praise. But there’s something even better: an even bigger picture. As mentioned earlier, the Unimap neither reflects everything that has been unified nor everything that still needs to be unified. This goes beyond the previously mentioned plurality in the Standard Model with its many particles and various attributes. For example, each constant of nature, such as the gravitational constant, the speed of light, Planck’s constant, elementary charges, the masses of fundamental particles (and many more), calls for a deeper understanding and further unification—similar to how the speed of sound was once considered a constant, but was later explained through the unification of the phenomenon of sound with the underlying kinetic movement of atoms. The same applies to matter and antimatter, different kinds of symmetries, the plurality implied by time (past, present, and future) and space (different locations), and much more. The Unimap hints at outstanding unifications with three question marks, however that area is much too small; if shown to scale, it would be many times the size of the entire Unimap. The next logical step would be to create a more comprehensive map that provides an overview of everything we know that still needs to be unified. And even this may not capture everything, as there are probably many more unknown unknowns.
In other words, there’s still a long way to go—which means there are good reasons to keep enrolling in university to study physics. Or maybe not?
Do today’s physicists have the broad mindset that is called for? As always, the answer is mixed: some have it more, some less. However, the following will argue that the average, traditionally trained physicist tends to be on the “some less” end of the scale. This may be a key reason why we’ve had almost no progress in fundamental physics in over 50 years, as reflected in the dates of discoveries on the Unimap.
A strong indicator of a currently lacking comprehensive view is that the Unimap had to be drawn up by a non-physicist in late 2024. While there has been a wide agreement that unifications play a key role for a long time, if you asked physicists to provide a map—or, to make it easier, just a list—of concepts that still need to get unified, their response would probably be limited to general relativity and quantum mechanics, as well as the four forces. If you’re lucky, they may mention the particles in the Standard Model too. And if they also state natural constants, you’ve hit the jackpot. The fact that unifying the four forces is considered the holy grail of physics may initially give a different impression, but we shouldn’t be fooled: unifications—holistically speaking—are not in focus in current physics.
The lack of a comprehensive view also becomes apparent when discussing the claim that there has been no progress in fundamental physics over the last 50 years.[19] If this claim were incorrect, it should be easy to refute—just one counterexample would suffice. However, the examples commonly cited miss the mark. The experimental confirmation of the Higgs boson in 2012 and gravitational waves in 2015, while impressive, did not contribute anything new to the underlying theories. Referring to advances in condensed matter physics, quantum computing, or nanotechnology suggests an oversight of the word fundamental in the original claim. More worryingly, some physicists have begun redefining what progress means (“No progress? No worries! Let’s just redefine it.”) by asserting that the further development of speculative theories constitutes progress in itself. However, the true measure of progress is the cross-check against experimental reality, not theories celebrating themselves. In any case, the main reason it sometimes feels like we are making substantial progress is that we are often deeply immersed in the details of incremental progress. A broader perspective can help to avoid falling into that trap.
Undoubtedly, a key reason for the lack of the big picture is that the level of specialization has significantly increased over the last few decades—a quest that has led to learning more and more about less and less. This contrasts with the mindset of the “old masters” who achieved unifications—be it Newton, Maxwell, Einstein, Heisenberg, Dirac, or many others—who had much more of a generalist approach to physics. In fact, their scope was so wide that it also included areas considered “philosophy” today, as mentioned above. This allowed them to succeed because unifications, by their nature, must occur on a higher level.
Another advantage generalists have is that they tend to be more knowledgeable about different problem-solving techniques across various domains, enabling them to apply those techniques to other areas. For example, Yang-Mills theory, while not initially developed with the strong nuclear force in mind, later proved instrumental in the unification of the electromagnetic and weak nuclear forces and eventually in describing the strong nuclear force through quantum chromodynamics. Fourier analysis, originally created to address problems in heat conduction, has since become foundational across many areas of physics, including quantum mechanics (for solving wave equations), signal processing, and the study of electromagnetic waves. Similarly, non-Euclidean geometry was a purely mathematical concept before Einstein applied it as part of general relativity. In a related vein, Heisenberg’s matrix mechanics, which employed the mathematical framework of matrices, revolutionized quantum theory. Such cross-field application of knowledge highlights the strength of generalists, who are able to draw upon insights from multiple domains and repurpose them for breakthroughs in new areas.
Incidentally, this may also explain why the same names keep reappearing across different domains in charts of progress in physics. As shown there, pioneers like Alhazen, Newton, Foucault, and Einstein made breakthroughs in entirely different areas. It seems unlikely they would reach such peak performances if there were no connection between those fields. Attributing their success to “just being great physicists” feels superficial. A more plausible explanation is that their success in different fields wasn’t due to brilliance alone, but rather that their broad scope across fields enabled their success in each one. This wouldn’t be possible with silo thinking.
Do today’s universities promote broad or specialist thinking? The fact that many people perceive this question as rhetorical is itself a clear answer. Students are typically required to specialize in subfields like quantum mechanics, condensed matter physics, or astrophysics early in their academic careers. Funding agencies tend to allocate resources toward specific, cutting-edge research projects within narrow fields of study, which further reinforces this specialization. The publication landscape in physics reflects this specialization, with academic journals dedicated exclusively to specific subfields. Finally, the job market often rewards specialists, as hiring in physics departments frequently centers on candidates with deep expertise in specific niches. In other words, universities produce what the market demands.[20]
Also, it makes sense to remind ourselves what a university is. At its core, a university is an institution designed to teach current knowledge to the next generation. To gauge how well it succeeds, it must assess students, which can only be done by testing them against what is already known (ideally with clear verdicts, such as “this is the correct answer, this is not”), essentially checking how well they’ve internalized existing ideas. This subtly conveys to students that current understanding is the truth, making it harder to question (and unlearn) later. Challenging existing paradigms—which is required for fundamental progress—isn’t only a different ballgame, but it’s the exact opposite. Simply put, universities are not designed to create revolutionaries, so they shouldn’t be blamed if they don’t.
However, not to let universities off the hook entirely, there are opportunities within their framework that could enhance the chances of fostering new ideas. Reducing the heavy emphasis on publications (“publish or perish”) and citations as measures of success could help, as these steer researchers toward popular, well-established topics with a higher chance of being published or cited, rather than exploring speculative niche areas—making everyone run in the same direction. The arbitrary criteria for what qualifies for academic credit (papers do, books don’t) and the frequent focus on the number of publications, rather than their quality (“The dean can count, but he cannot read”) also set the wrong incentives.[21] On the positive side, some professors encourage students to engage in research by assigning projects rather than final exams. This allows for more creativity, and this approach should be expanded, along with a focus on teaching methods over mere outcomes.
Without a doubt, universities can add significant value by providing a strong foundation of knowledge and essential tools like mathematics. But they are designed to convey the currently known rules, not to break them. Their high level of specialization risks discouraging the high-level thinking required to discover new unifications. Additionally, there are other crucial qualities that are difficult to teach at a university…
When looking at the Unimap and the Big Four theories, one thought immediately comes to mind: the creators of those theories must have been incredibly bold. They didn’t just challenge one established paradigm but several at once. Achieving this goes beyond intelligence; it requires free-spirited thinking and a good amount of courage. This hints at a crucial factor often overlooked in academic physics: personality.
Personality also plays a role in the generalist vs. specialist debate. When criticizing universities for their focus on specialization, this might suggest that universities could simply “change their production line” and start turning out generalists instead of specialists. But it’s not that simple. Generalism and specialism stem from fundamentally different mindsets rooted in individual nature. Specialists focus on differences, while generalists look for similarities and patterns—the precursors to unification. Generalists tend to seek out new opportunities, while specialists prioritize precision and avoiding errors. While optimism can benefit specialists, it’s essential for generalists, who naturally take more risks and feel more comfortable with uncertainty.
From this, it can be concluded that generalists are more inclined to explore new, uncharted territory, often leading rather than following. It also suggests they will always be in the minority; spearheading progress is, by definition, the work of the few. Groupthink leads to conformity, which rarely fosters characteristics like boldness, leadership, or intellectual independence. Not only were many of the biggest advances made by individuals, but these individuals were often physically separated from mainstream academia. Newton’s “miracle year” (annus mirabilis) in 1666, during which he made groundbreaking contributions to calculus, optics, and the laws of motion and gravitation—essentially laying the foundation of modern science—took place while he was isolated at home during the Black Death. Similarly, Einstein’s miracle year in 1905, during which he published several revolutionary papers (on the photoelectric effect, Brownian motion, and special relativity), occurred while he was working as a patent clerk in the Swiss patent office, far removed from the academic establishment.
If these two scientists, arguably the greatest who ever lived (accounting for three of the Big Four theories in the Unimap), succeeded in this pinnacle of human achievement—from a historical pool of around 100 billion people—then it’s no longer reasonable to ask how they succeeded despite their separation from academia; it would be far too unlikely for them to have done so with major obstacles in their way. At the very least, we must ask why this separation didn’t hinder them, or, more appropriately, how such ostensible obstacles may have even helped. Viewed from this angle, it starts to make sense.
If groups—be they institutionalized groups like universities or any other—can negatively impact free thinking, it suggests that group-seeking traits may also have drawbacks. Many top theoretical physicists, in fact, lean toward introversion rather than extroversion. This makes it easier to break from social norms, which can be either positive—when the goal is to explore new ideas—or negative: it’s often said that there’s a fine line between genius and insanity.
Free thinking also enables another crucial ingredient for progress: creativity. Intelligence allows us to move quickly within a set of rules, but real breakthroughs, as the word says, come from breaking through them. Traits like curiosity, playfulness, and even child-like wonder are key. The free and uninhibited moving around of concepts to find unifications—such as “Could force be the same as matter?” or “Could matter be just a form of spacetime?”—must appear, to the traditionally trained physicist, like the pinnacle of crackpottery. But, in fact, it’s an essential exercise in brainstorming and creativity.
On a side note, humor often signals a creative mindset. An enjoyment of surprising twists—on which humor often hinges—may reflect openness to similar twists in physics. Self-deprecating humor, in particular, shows a healthy willingness not to take oneself or one’s theories too seriously, allowing for quicker course corrections when evidence points in a different direction. In addition, humor can make life—and physics—more enjoyable, creating a conducive environment for peak performance. Many top physicists had a keen sense of humor.[22]
Lastly, the role of humility should be emphasized, as it is a key trait in the scientific endeavor. As Karl Popper showed, science offers no proof—only falsification—echoing the “we can only be less wrong” concept mentioned earlier. This naturally fosters humility, which is crucial for discovery. The insight “It’s actually the same”—which is unification in other words—doesn’t come from fanciful thinking but from an attentive, patient, and humble mindset. The loud, flashy physicist who confidently declares the world to be like X or Y will overlook the subtler truths that reveal themselves only to those willing to pause and listen.
There’s much more to be said about physicists’ personalities (see Profiling Top Physicists and Physicists Are People Too), but that goes beyond the scope of this article. For now, one more question needs addressing: If these traits are so important for progress in physics, why aren’t they emphasized in physics education? One reason is that they’re difficult to measure. IQ, whether tested directly or indirectly through university exams (which are often IQ tests under a different name), provides a precise score on a standardized scale. This clarity can be seductive, as we often give more weight to what we can easily measure. Another reason, as mentioned earlier, is that many of these traits are hard to teach. However, we must know what qualities to aim for to cultivate them. The next big breakthroughs—whatever they may be—will require not just top intellectual performance, but also peak performance in terms of personality.
As mentioned above, questioning existing models is required, but difficult. To succeed at it, we need to understand how deeply rooted our models are and the specific ways they influence us. Otherwise, they will continue to slip into our thinking without us realizing, thereby preventing progress.
The language we’re using can be an indicator that we’re relying on our old models. Often, we use everyday words to describe phenomena they weren’t meant for. This may lead us to believe that those phenomena are similar to those in our everyday world. The risk of this happening comes in various degrees. It probably goes without saying that elementary particles don’t taste like much, so they don’t actually have any flavors, or that gluons, which bind together quarks (that don’t have any color), don’t need a lot of glue to work. Likewise, particles don’t need to fear being bullied for being left-handed.
However, there is a chance that an educated non-physicist or philosopher believes that elementary particles spin around their axis like basketballs or orbit the atomic nucleus like planets around the Sun. Always popular are the beliefs that light is both a wave and a particle, that particles have mass in the conventional sense of weight, and that space can be truly empty. Even if they succeed at questioning the old model, they may still express it in classical terms, such as believing a particle can exist in two locations simultaneously (“superposition”). All these notions are fundamentally incorrect, stemming from our tendency to view the world through the lens we’re born with. If we have a hammer, every problem looks like a nail, but it may lead us astray.
Even physicists are not immune to falling into this trap. While many intellectually understand that quantum mechanics doesn’t behave like classical mechanics, the mental picture many still hold is of something moving through space as time elapses, a notion supported by models like Feynman diagrams. The idea that forces must act on something—if not a particle, then a field—is also a remnant of our old model. Or, we might think we’re leaving the macroscopic world behind to explore the microscopic, without realizing that it still includes many of the same assumptions, as the small is often seen as merely a “zoomed in” or “chopped up” version of the large. Our old assumptions slip in so easily that they are very difficult to catch.
If we stand on such wobbly ground, do we even have the chance to come up with better alternatives? Surprisingly, in the first step, we may not even need any. It’s already valuable to know which approaches aren’t heading in the right direction. If we keep in mind the shortcomings of our old models and then hear about theories postulating fundamental reality consists of “little strings, either loose like ropes or formed into circles like hula-hoops,” it immediately doesn’t sit right with us. Even if we don’t have any alternative theories yet, there is value in knowing which theories probably take a wrong approach, saving time to focus on more promising ones.
But at some point, we need to think about alternative models. How is it possible, considering that as soon as we think, talk, and especially when we visualize, it’s automatically based on our old, flawed model? Is there any way we can escape our cage? Surprisingly, even if we cannot, it doesn’t mean that progress is impossible. As mentioned before, the key lies in making our old models less wrong. The new understanding may appear as an entirely different theory, but the underlying reason why it is better is because it removes flaws—mostly distinctions, through unifications—in our old models.
For example, let’s take the original understanding that particles have a distinct location in three-dimensional space. This model implies a lot of plurality: every point in the universe is a potential location for a particle. If we instead postulate that particles are waves with a two-dimensional wave front[23], this plurality is significantly reduced, effectively removing two dimensions. While this may seem like a new theory (“Wave theory of matter,” with a capital W), it could also be seen as a mere unification and reduction of complexity in the old model. The next logical step is the concept of a field, which removes the remaining dimension entirely (which, incidentally, also suggests that it might be less about particles and more about dimensions themselves).
This is also a good example of how we continue clinging to our outdated models. The very term “particle,” in its intuitive sense, implies something located at a definite position. As soon as we say, “a particle behaves like a wave,” the concept of a particle “waves out of existence,” bidding farewell as a construct we need to give up. Similarly, regarding particles as fields, which essentially means “a particle is spread out in space,” is, in a way, to say, “a particle is not a particle.” While there’s truth to that, we struggle to let go of these familiar terms, even after they’ve been refuted. It’s like the concept of spacetime—once tied to familiar ideas of space and time—but now it’s something altogether different. Likewise, space doesn’t really bend, as general relativity suggests; something else is happening, but it appears as though space is bending when seen through the lens of our old concepts. We’re patching a broken framework, which is understandable since we have no better alternative. But it’s crucial to remember that we’re not describing reality itself, only the shadows cast by a deeper truth.
It’s interesting to examine physicists’ relationship with current models. On one hand, there’s broad agreement with the idea that our theories are temporary and subject to improvement. The well-accepted statement “our theories are only as good as we find better ones”—which doesn’t show a lot of confidence in current models—reflects this sentiment. On the other hand, physicists often ascribe a degree of truth to the language and concepts they use. For instance, matter—undoubtedly an important component of our models—is frequently treated as though it exists independently of the models themselves. This may stem from the difference between rational understanding and emotional acceptance. In any case, there’s still room for further reconciliation between these two perspectives.
Letting go of our current models must not be confused with the permission to go completely nuts. There’s always the risk that in breaking away from our current models, we might end up making things up. This usually adds more complexity and plurality, which is the opposite of unification. That’s why progress in physics is primarily a process of discovery rather than invention. A parallel can be drawn with literature: good fiction writing is often not fiction in the sense that it’s entirely made up. Talented writers don’t invent so much, but they find so much. This makes their work ring true on a deeper level that fabricated stories cannot achieve. Most good fiction is autobiographical, at least to some extent (Flaubert: “Madame Bovary, c’est moi!”).
There are several reasons why we get drawn to the fancy. First, it appeals to our ego—we enjoy thinking, “I was able to come up with something that complex.” Second, complex theories are harder to refute, which we sometimes mistake for a sign of truth. Third, the spectacular can make flashier headlines, and seem more likely to be correct, which is why people overestimate the likelihood of winning the lottery or dying in a plane crash. Fourth, if we created something complex, we’re more likely to identify with it, making it easier to fall in love with our own ideas.
There’s also the misconception that if a theory seems crazy, it might hold some truth, since past theories that turned out to be closer to the truth were initially seen as crazy too. However, this logic could be applied to anything, so it cannot be valid. At best, it’s an argument against the argument that a theory must be wrong solely because it seems crazy—but it’s never a direct argument in favor of the theory itself.
Complicated models can also seem attractive because they often explain more. Every new epicycle added to the Ptolemaic model helped it match observations more closely, making it appear more successful. However, we now understand that these were just patches on a fundamentally flawed model. It’s often possible to improve a model’s accuracy by adding variables, but in fundamental physics, true progress typically moves in the opposite direction—toward greater simplicity and unification.
The urge to go all out often stems from a desire to break radically from current models. On one hand, this is well justified. On the other, if progress means fixing flaws in our old models, we can’t stray too far. To put it visually, if we set sail to explore the open ocean, we should keep the shore in sight. That’s also because the old, flawed theories can be stepping stones to better ones—without Ptolemy’s geocentric model, we might not have had Copernicus’ heliocentric breakthrough, and the same for Newton’s classical mechanics and Einstein’s theory of relativity. It’s a bit like in judo, where you need a good grip on your opponent to flip them over; as the saying goes, “Keep your friends close, but your enemies closer.”
Such apparent paradoxes—radically abandoning old models while keeping them in view—might be the true challenges of progress. To manage those, personality is crucial once again. We must allow seemingly contradictory ideas to co-exist in a kind of “superposition,” resisting our instinct to resolve the discomfort of uncertainty. We need to think freely and break from established mindsets while exercising enough self-control to avoid excessive speculation. We must think boldly and on a grand scale, yet remain careful to avoid the trap of over-assumption, staying attuned to details and subtleties. Optimism is essential to explore the unknown, but we must remain rigorously critical of our own approaches.[24]
Perhaps this is the real reason why progress is so difficult: no single approach, however optimized, is sufficient on its own. We must make room for mindsets that seem contradictory. This is further elaborated in the OPIP book.
One type of fancy deserves special mention due to its prevalence in physics: the endless extrapolation of phenomena, assuming that things can go on forever—i.e., the concept of infinity. As mentioned before, infinities are the opposite of unification and should therefore be avoided at all costs.
It’s interesting to observe physicists’ relationship with infinity, as it’s somewhat paradoxical. On one hand, it’s well-accepted that when infinities arise, it indicates that something in the theory is flawed. Indeed, resolving such infinities brought major progress: Planck’s introduction of the quanta solved the infinities of energies emitted by a black body (“ultraviolet catastrophe”), laying the foundation for quantum mechanics—which has since involved numerous removals of infinities, from regular quantization to renormalization in quantum electrodynamics. Similarly, Einstein’s general relativity solved the issue in Newton’s gravity that postulated that the gravitational force becomes infinite at zero distance between two masses. There are many more such examples.
On the other hand, many physicists postulate the existence of actual infinities in various areas of their theories. Some propose an infinitely large universe or one that expands forever (“eternal inflation”). The universe’s lifespan is also often considered endless (or, like the “cyclic universe,” that it goes through never-ending loops of expansion and contraction). General relativity’s prediction of singularities inside black holes—regions of infinite density—is likewise taken literally by some. It would also be remiss not to mention string theory, which sometimes treats certain infinities as real features. There are many other examples, but they all pale in comparison to the “multiverse” theories that often posit an infinite number of parallel universes—which must be the unificationist’s worst nightmare.[25]
The fact that infinities have never been observed in practice already gives them a whiff of having been invented by humans. Moreover, it’s impossible to observe or validate them in practice in principle. Why, if they cannot occur in the reality we live in, are they sometimes postulated as part of our reality? Infinities should also be viewed skeptically as they reflect a deep belief in our old models—simply extrapolating them with “just like this, only never-ending.” However, history has repeatedly shown us that progress in fundamental physics has never been “the same, just more,” but always “different, and less.”
Why do infinities remain so popular in physics? Several factors seem to contribute to it: First, it’s yet another sign that many physicists haven’t fully internalized the importance of unification. Second, the tendency to favor more abstract or “fancy” ideas likely plays a role as well. Third, infinities can provide an easy way out; if a quantity isn’t infinite, it requires an explanation for why it takes a specific value. Lastly, there’s a simple reason: a lack of checks and balances. Infinities tend to crop up in theories that are far from being falsifiable, giving physicists a sense of theoretical freedom that may not be fully justified.
However, there’s good news too. If infinities can’t be right, they offer a clear path to improving our theories: we simply comb through them, find where infinities pop up, and resolve them—making our theories simpler and more beautiful, which history suggests is essential for making theories less wrong.
There seems to be a misconception about the role of “beauty” in fundamental physics, a concept that many physicists have emphasized to varying degrees. This ranges from recognizing that beauty plays some role (Weinberg: “Physicists feel a powerful aesthetic impulse to build theories in which everything fits together beautifully”), to viewing it as an indicator of a good theory (Feynman: “You can recognize truth by its beauty and simplicity”), to placing it on the same level as observations (Einstein: “The theory must not only fit the facts, it must be beautiful”), and, for some, even prioritizing it over experimental results, as expressed by Dirac (“It is more important to have beauty in one’s equations than to have them fit experiment”) and Weyl (“My work always tried to unite the true with the beautiful, but when I had to choose one or the other, I usually chose the beautiful”).
However, the truth doesn’t always appear more beautiful. For example, the Ptolemaic model (the geocentric model with Earth at the center) used beautiful circles to describe planetary orbits, while Kepler revealed that these orbits are actually “ugly” ellipses in the heliocentric model.[26] Similarly, the implications of quantum mechanics or relativity theory—particularly its non-Euclidean geometry, which contrasts sharply with the beautiful Euclidean geometry of straight lines and perfect angles—are often seen as strange and unintuitive, lacking a sense of beauty.
That we should be skeptical about beauty is evident from the fact that it’s so subjective; different people perceive different things as beautiful, so it cannot serve as an objective guide. This becomes particularly clear when the physicists’ personal relationship with their theories comes into play. Many see their theories as their brainchildren; and like a mother with her ugly baby, they think it’s the most beautiful in the world. For this reason, it’s crucial for both creators and the community to separate the theory from the creator, or the art from the artist, as discussed in the OPIP book.
So, what’s the conclusion: does beauty now play a role or not? The resolution lies in diving deeper into how the feeling of beauty arises. If we start out with monstrous equations, and then Einstein comes along and boils it down to E=mc2, we perceive it as beautiful.[27] In this case, beauty was a result of increased simplicity, or its causal agent, which is unification. Hence, beauty was a good indicator. However, the feeling of beauty can be triggered in many other ways too, and it would be a mistake to then attribute truth to those cases as well. Moreover, even if the feeling of beauty was triggered by unification, it still doesn’t mean the theory is correct, as not every unification is valid. In other words, beauty can be seen as a requirement for a good theory, but it is far from sufficient, as shown in the following chart.
That beauty and simplicity are crucial can also be gleaned directly from the Unimap: it’s incredibly easy to understand. Isn’t that remarkable? The Unimap captures the pinnacles of human ingenuity, yet you don’t even need a PhD to grasp it. Admittedly, the Unimap does simplify certain details. It omits countless contributions, many minor discoveries leading to major ones, and the intricate relationships between those discoveries. It also doesn’t show the experimental challenges, the complex mathematics involved, the journey to these discoveries, and the setbacks. But the final outcomes are in the Unimap. It’s not a dumbed-down version so that the everyday person can get a simplified, but essentially distorted and inaccurate, idea of what is going on. No, the key insights remain intact in the Unimap. The same is true for other charts about progress in physics, further corroborating the power of beauty and simplicity.
What is the goal of physics? For many, it’s to find the underlying principles that explain “everything we can see or measure.” At first glance, this seems like a bold goal because it includes the term “everything.” However, the scope becomes dramatically narrower when we shift our focus from “everything” to “what we can see,” as there could be many phenomena that we haven’t yet experienced. Today, physics often takes a reactive approach, racing to explain phenomena we don’t yet understand. On one hand, this is understandable, as such phenomena reveal where our models fall short. However, it remains fundamentally limited to what we have observed so far.
The realization that unification drives progress offers a new angle: any distinctions we make in our models reveal flaws that demand resolution. As long as these distinctions remain, we should never be satisfied, even if our theories explain everything we can currently observe or measure. This perspective also brings a renewed sense of hope. When Heisenberg expressed doubts about further advancements in fundamental physics, his concerns were rooted in the well-founded belief that reality may be beyond human comprehension. While this article agrees with his premise, it disagrees with the conclusion. If progress is driven by unifications, then it suddenly seems much more attainable—because it simply involves reversing the flawed distinctions we created ourselves. It feels like we have a new “grip” on a problem that previously eluded us.
The philosophy behind this approach can also be described as focusing on the path rather than the outcome. It’s true that, in the end, we need models that make accurate predictions that we can measure or experience. However, focusing directly on those may not be the best approach. It’s as if we wanted to reach places A and B, and came up with very specific solutions which nobody asks about once we arrive. Instead, we should focus on developing the engine that, like a car, will then also take us to places C, D, and E we never knew existed. In fundamental physics, unification is that engine.
How can we focus on the engine? First, simply staying aware of the importance of unification will help us naturally gravitate toward it. Second, we should take the steps outlined above: expand the Unimap to include all the different concepts that still need to be unified; think holistically, not just about the unification of forces; search for plurality—especially infinity—in our existing theories, and replace it with new concepts; and prioritize unification attempts for concepts that have already shown some form of connection (dotted lines in the Unimap).
We may also want to give more room to theories that have already taken the path toward unification. Ironically, some theories—such as timeless theories (which remove the distinctions between past, present and future) or non-local theories (which eliminate the distinction of different locations)—may already be on the track of unification without fully realizing it. Additionally, analyzing past theories through the lens of unification could deepen our understanding of their successes while further corroborating the importance of unification itself.
Finally, we must continue to pay attention to the secondary contributors to progress, which aren’t secondary at all: since physics is done by people, personality plays a key role. This includes the courage to take new approaches, the independence to think beyond existing frameworks, and a generalist, “big picture” perspective. Playfulness and creativity are essential too. And above all, humility is required; the hardest thing to accept is that unification implies that our understanding of the world is fundamentally wrong. The old masters seemed to have been right: as Socrates said, “I know that I know nothing.” In any case, we shouldn’t get hung up on that thought—let’s just hold our nose, swallow that pill, and think about its conclusions. We’ll be rewarded profoundly for it.
—
[1] This is emphasized by the fact that various religions hold the belief that each object, whether living or non-living, possesses its own distinct soul (so-called Animism).
[2] The four forces that physics aims to unify are the electromagnetic force, the weak and strong nuclear forces, and gravity. It’s worth noting that the term “four forces” remains in use, even though the electromagnetic and weak nuclear forces have already been unified under the electroweak theory. Thus, the actual goal should be articulated as unifying the three remaining forces. However, this article will follow the historical convention of referring to the unification of all four forces rather than three.
[3] This idea is also a first step toward unifying the different methods of unification by revealing their underlying commonality or even equivalence. This can occur in subtle ways. For example, let’s consider the concepts of a horse and a unicorn. If it’s discovered that unicorns don’t exist, it may seem like a case of unification by eliminating the concept altogether, without touching the other concepts, as described in the third type above. However, the definition of “horse” implicitly includes the notion of “not a unicorn.” Thus, when we discard the concept of a unicorn, it impacts how the term “horse” is used, even if only slightly. More on the unification of methods further below.
[4] This must not be mistaken for an endorsement of specific symmetry-based theories in physics (e.g., supersymmetry), as many other factors play a role in the holistic assessment of such theories. It only acknowledges that symmetries can, under certain circumstances, serve as one possible step closer to unification.
[5] For future generations: Taylor Swift was a popular singer at the time this article was first published.
[6] Insects are often depicted as stupid. However, “stupid” in this context simply means that they couldn’t perform the tasks we need to accomplish in our world. The thing is: we also couldn’t do the tasks in their world. The value of a model must always be assessed within the context in which it is applied, as elaborated further below. Similarly, while an insect will never grasp our understanding of the world, could the reverse also be true?
[7] Rifkin, S.A. et al (2003): “The Evolution of Gene Expression in Drosophila melanogaster” (Nature Genetics).
[8] Newton’s laws of motion and his law of universal gravitation are fundamentally enough to describe the principles needed to send a man to the Moon. However, the actual achievement required many technologies that go far beyond Newton (e.g., quantum mechanics for the transistors and semiconductors in modern electronics).
[9] The term paradigm shift was introduced by Thomas Kuhn in his influential book The Structure of Scientific Revolutions from 1962. In it, Kuhn challenges the traditional view of scientific progress as a steady, cumulative acquisition of knowledge. Instead, he posits that science undergoes periodic paradigm shifts where a prevailing scientific framework is replaced by a radically different one. The release of the book was a landmark event and sparked controversial debates across many disciplines.
[10] Taking only bees as an example: there are more bees than humans (an estimated 2 trillion vs. 8 billion), and they have been around much longer (approximately 130 million years vs. 300,000 years). Evolutionarily speaking, they got us beat, big time. Moreover, time seems to be on their side. Humans, with their self-destructive capability in the form of nuclear weapons or environmental devastation, as well as a higher vulnerability to external catastrophic events such as asteroids hitting Earth, may turn out to be an evolutionary dead end, as it has been the case for 99% of species. For sure, I’d put my money on the bees.
[11] Studies show that men tend to score higher than women on measures of narcissism, which is often related to ego. A meta-analysis by Grijalva et al. (2014) reviewed over 355 studies involving nearly 500,000 participants and found that men were more likely to exhibit narcissistic traits, particularly in the domains of entitlement and leadership/authority. Additionally, men tend to be more ego-defensive in certain contexts, especially when their competence or social status is challenged. For example, Scheepers & Ellemers (2019) discuss this defensiveness in their study on status stress, while Terrell et al. (2008) examine gender differences in aggression and the role of status in competitive interactions.
[12] The exact Max Planck quote from his autobiography is, “An important scientific innovation rarely makes its way by gradually winning over and converting its opponents: it rarely happens that Saul becomes Paul. What does happen is that its opponents gradually die out, and that the growing generation is familiarized with the ideas from the beginning.”
[13] The solutions are not only surprising to those who they are presented to, but to the discoverers themselves too. Newton in a letter to Bentley in 1692: “That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one to another, is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it.”
[14] In The Grand Design (2010), Hawking stated: “Some people believe that there is a single theory that explains everything. It is called the theory of everything. That is what Einstein was trying to find. But we now believe that the search for such a theory is misguided.” Similarly, Dyson, in New Scientist (2004), remarked: “I have the feeling that in physics, we don’t need something as final as a theory of everything.” Other physicists, such as Heisenberg, also made similar remarks, which will be addressed further below. Additionally, it should be noted that the skepticism surrounding future unification is often fueled by the observation that we’ve been searching for it for over 100 years without success. However, this view is somewhat myopic; 100 years, while it may feel significant, is historically a very short period of time.
[15] A frequent objection to the possibility of further unifications is that just because unifications have occurred in the past, it’s an assumption that they will continue. While this is true, the only alternative would be to postulate that unifications have happened throughout history but will now suddenly stop for the very first time. That seems like a far bolder and more speculative assumption. History suggests otherwise.
[16] The phenomenon of a self-centered worldview, especially in the more southern of the two stated countries, seems to recur frequently—also outside the field of sports. The country’s very name could be seen as a reflection of this mindset, as it suggests a claim to an entire continent. This attitude should be kept in check; otherwise, there’s a real risk that one day a politician may officially declare their country to come first.
[17] Weinberg, S. (1994): Dreams of a Final Theory: The Scientist’s Search for the Ultimate Laws of Nature
[18] This doesn’t rule out the possibility of string theory being closer to the truth, as the increase in conceptual elements might only be temporary. However, once you open Pandora’s box and let out many different dimensions, you’ll need one hell of a theory to catch them all and unify them again.
[19] It could even be argued that we haven’t achieved any major progress in fundamental physics over the past 100 years, though this depends on how one defines major. In terms of impact on our everyday life, the advances of the past 100 years certainly deserve that label. For instance, Quantum Electrodynamics (QED) paved the way for nanotechnology, which underpins much of today’s technology (without which you couldn’t read these lines). However, in the broader context of unification, the picture changes. QED largely extended the ideas set in motion by quantum mechanics, unifying only a limited number of concepts. Similarly, the prediction of the Higgs boson wasn’t a unification—it merely added another particle to the Standard Model, which already includes nearly 50 particles (counting antiparticles). The reason the Higgs boson’s discovery seems groundbreaking at first might be due to the absence of truly revolutionary developments like those in the early 20th century, which gave us relativity theory, quantum mechanics, and nuclear physics. This phenomenon is well-known in psychology and is often described as the “context effect,” where perception is influenced by surrounding factors. The fact that it wasn’t truly groundbreaking also becomes clear if we consider the literal meaning of the term. The discovery of the Higgs boson continued on existing ground—the Standard Model—and didn’t break it.
[20] For those who object to the statement that universities “produce what the market demands” by pointing to fields like fine arts, philosophy, anthropology, archaeology, sociology, or gender studies: to my defense, I was only referring to the market forces that influence how universities respond to demand in certain fields, not making a sweeping assertion about the practical applicability of all degrees.
[21] “Incentives” might be the key word in this discussion. As Charlie Munger, the American investor, said, “Show me the incentive system, and I will tell you how people behave.” If pursuing niche areas leads to no citations, limited funding, and significantly worse job prospects, it effectively equates to career suicide. The issue lies in the system, and we should be cautious about blaming those who are simply playing by the rules of the game. That said, there must also be individuals who have the courage to question those rules to bring about change.
[22] While many 20th-century physicists displayed a great sense of humor (Einstein, Feynman, Bohr, and many others), one of them stands out: George Gamow. The Soviet-American polymath was renowned for integrating humor into his professional work. For example, he humorously asked Hans Bethe, another highly influential physicist, to co-author a very important paper that Gamow’s student Ralph Alpher wrote, despite Bethe’s lack of direct involvement in the research. This whimsical addition meant the paper’s authors would be “Alpher, Bethe, Gamow,” a play on the first three letters of the Greek alphabet. Gamow’s playful approach also made him a great teacher, who could make complex scientific concepts understandable and entertaining for a broad audience. His popular science books 1 2 3 Infinity and his Mr Tompkins series are highly recommended reading.
[23] This postulation deviates from the historical understanding in physics. When de Broglie discovered matter’s wave-like behavior, it was already conceived in three dimensions. The purpose here, however, is not to retell physics history accurately, but to illustrate a principle.
[24] It’s like chess, where beginners often try to find reasons for why their candidate move is good, while grandmasters do the opposite: they look for reasons it might be bad. They only play a move if they can’t find a refutation for it. It’s a more critical, “negative,” and psychologically difficult approach, but it’s more successful. For more parallels between physics and chess, see The Creative Process and Parallels Between Physics and Chess.
[25] To counteract the nightmares, the unificationist may find some relief in taking it with a dose of humor. For instance, when an “infinity of infinity” is seriously proposed in discussions like this, followed by the mild acknowledgment that there is “some criticism of that,” it shouldn’t fail to crack up the unificationist. Concepts like these don’t exactly hover in the grey area between science and non-science, as stated. Hence, the video’s title containing “cutting edge” is only accurate in the sense that it erases edges entirely, proposing that no boundaries exist at all.
[26] It should be noted that Kepler’s model of elliptical orbits contains a lot of beauty when viewed from the right perspective, as it replaced the far more complicated system of numerous epicycles in the Ptolemaic model. This highlights the idea that beauty is in the eye of the beholder.
[27] Although here again, it’s not a given that everyone perceives it that way, as beauty is subjective. If you had been a competing physicist with a deep disdain for Einstein, you might have found E=mc2 not only wrong but also the ugliest thing mankind has ever created. Once again, psychology plays a key role.
